总结
介绍了整数类型存储的方式,就 signed 与 unsigned 进行展开
字节、位、进制
基本知识
1字节(byte)=8位(bit)
字节大小为0~255
数字进制的记忆:
| B(2) | 1010 | 1100 | 1111 |
|---|---|---|---|
| D(10) | 10 | 12 | 15 |
| H(16) | A | C | F |
字节顺序
一个 int 类型的数据占 4 个字节
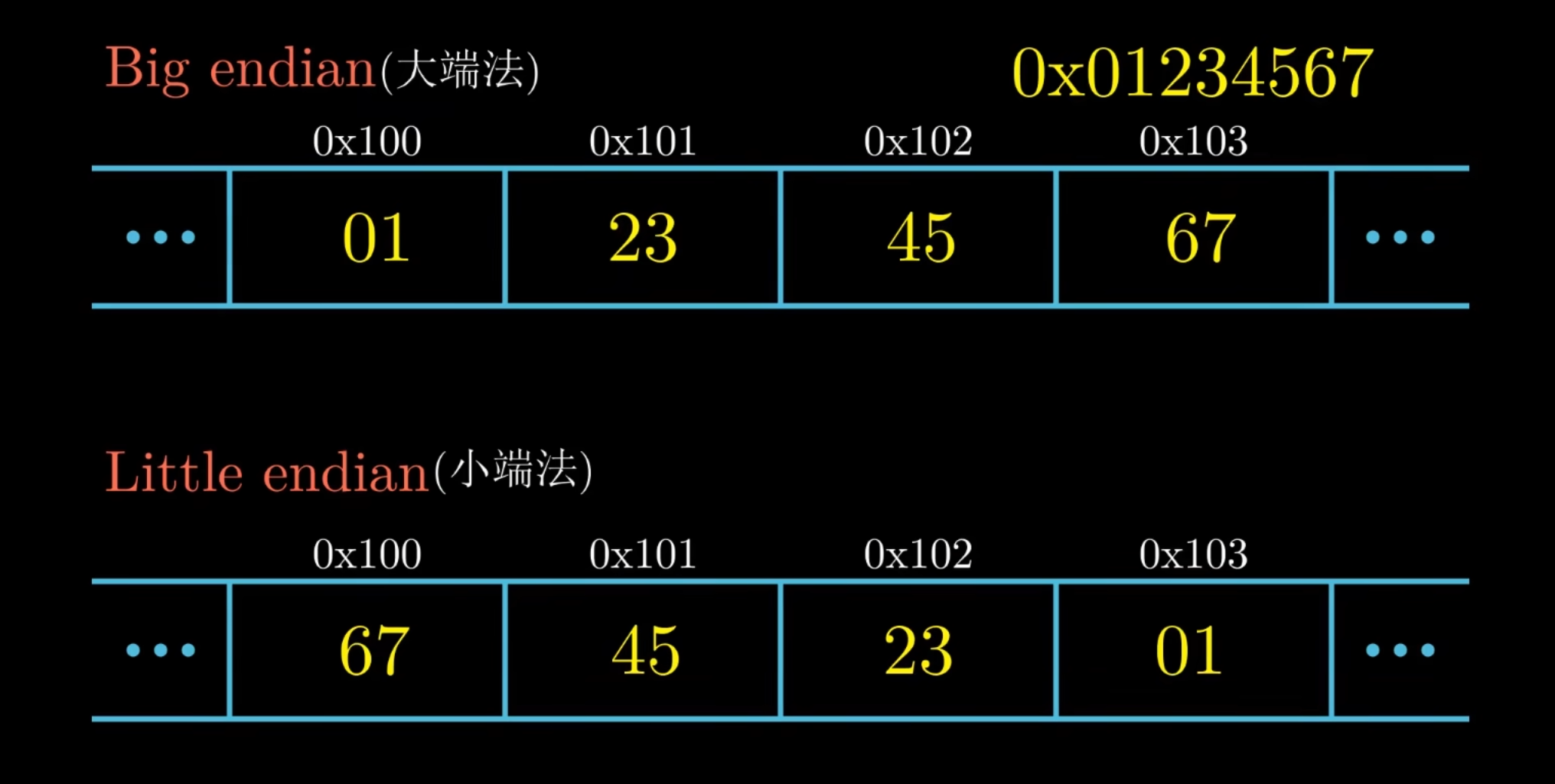
多种运算类型
布尔运算
~ (非)、& (与)、| (或)、^ (异或)
掩码运算
可以利用位运算的技巧来实现一些操作
掩码运算是位运算的一种常见应用,主要用于提取、设置或者反转整数中的指定位。一个掩码(mask)是一个二进制数,它的位模式指示了要对另一个二进制数进行的操作。以下为一些常见的应用:
提取位:使用位与运算(
&)和一个掩码,可以提取一个数中的特定位。掩码中的1表示我们感兴趣的位,而0表示我们不关心的位。例如,如果我们想提取一个字节的低4位,我们可以使用掩码0x0F(二进制为00001111),通过与原数进行位与运算,结果就只保留了低4位。设置位:使用位或运算(
|)和一个掩码,可以将一个数中的特定位设置为1。在这种情况下,掩码中的1表示要设置的位。例如,要将一个字节的最高位设置为1,可以使用掩码0x80(二进制为10000000)与原数进行位或运算。反转位:使用位异或运算(
^)和一个掩码,可以反转一个数中的特定位。掩码中的1表示要反转的位。例如,要反转一个字节中的最高位,可以使用同样的掩码0x80与原数进行位异或运算。清除位:要清除(即设置为
0)一个数中的特定位,可以使用位与运算和一个掩码,这个掩码在我们想要清除的位上是0,其他位上是1。例如,要清除一个字节的最高位,可以使用掩码0x7F(二进制为01111111)与原数进行位与运算。
通过这种方式,掩码运算允许我们在不影响其他位的情况下,对整数的特定位进行精确控制。这种技术在底层编程、硬件控制、网络协议设计等领域非常有用,因为它可以直接映射到硬件操作,提高程序的效率。
逻辑运算
! (非)、&& (与)、|| (或)
逻辑运算具有短路特性
| |
移位运算
左移(< <):丢弃最高的位,最低位空缺的补零
右移(> >):
1.逻辑右移[无符号数 unsigned]:同左移。丢弃最低位,最高位补零
2.算数右移[有符号数 signed]:最高位 =0 时,效果等同于逻辑右移;最高位 =1 时,最高位补 1
整数的表示
无符号数unsigned 与 有符号数signed 的取值范围
无符号数(unsigned) 的范围:$[0,2^{w}-1]$
有符号数(signed) 的范围:$[-2^{w-1},2^{w-1}-1]$
有符号数(signed) 的最高位的权值是 $-2^{w-1}$
无符号数(unsigned) 的最大值
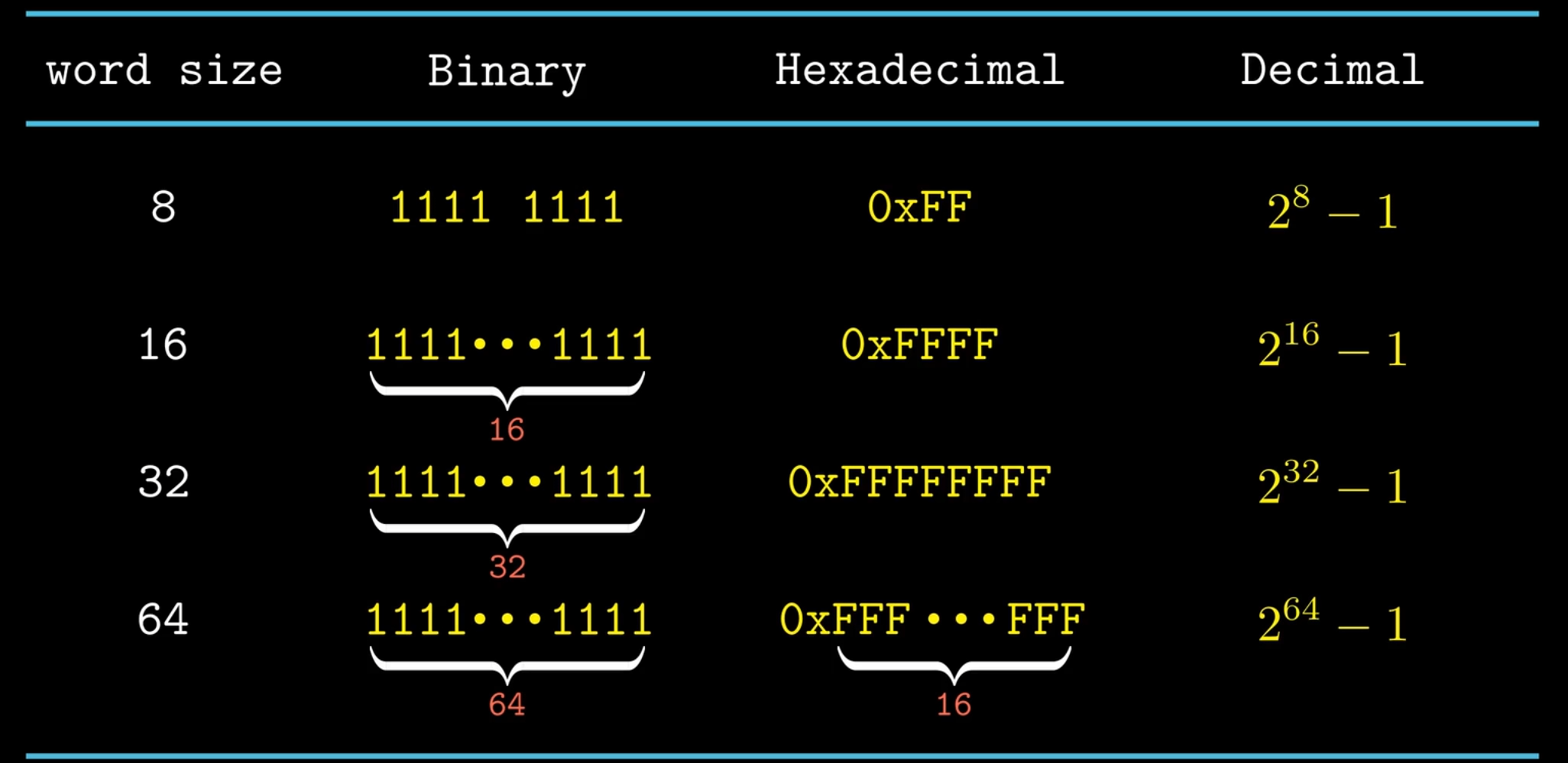
有符号数(signed) 的最大值
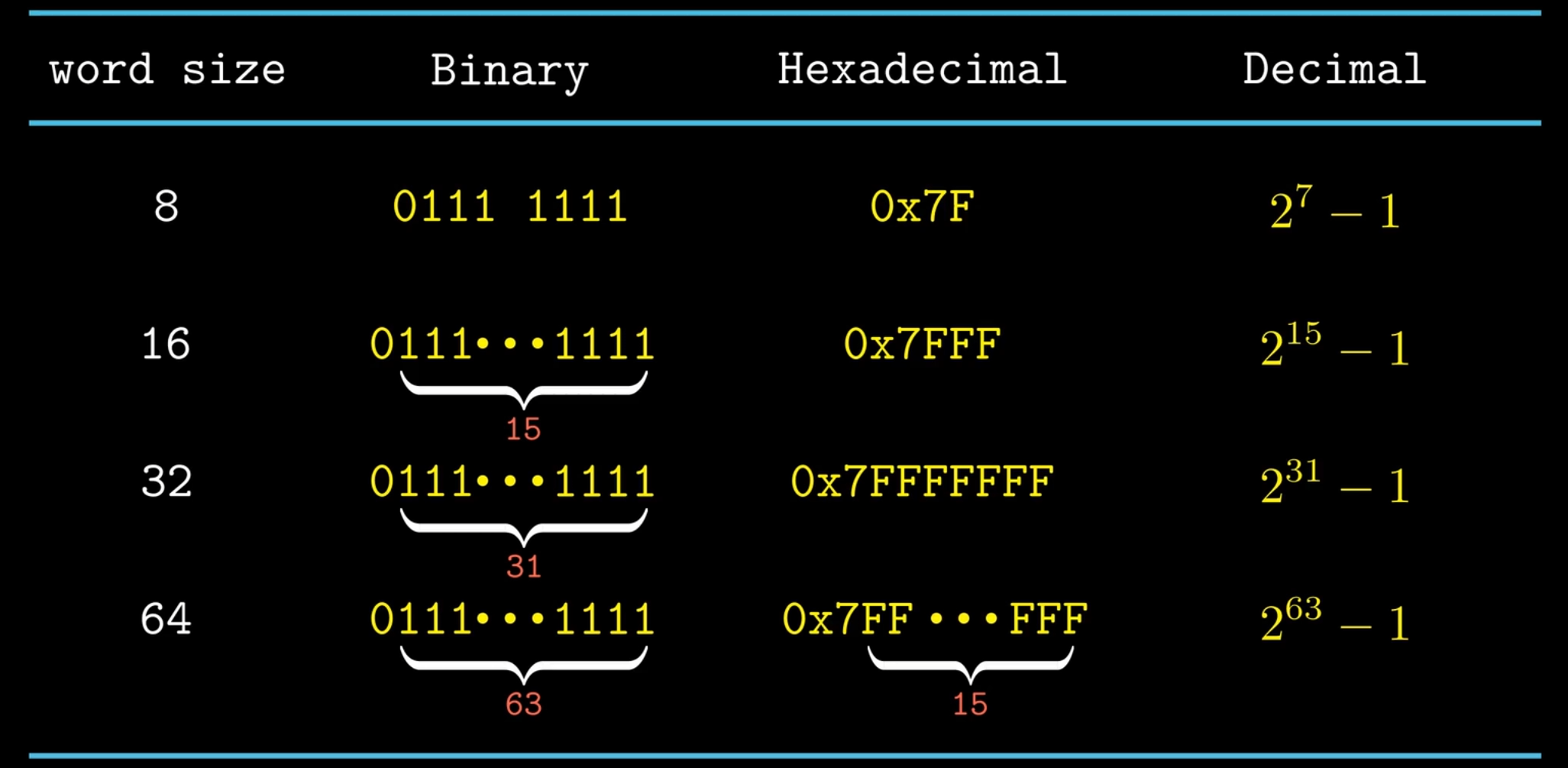
有符号数(signed) 的最小值

注意,有符号数(signed) -1 的表示与无符号数(unsigned) 最大值的表示相同
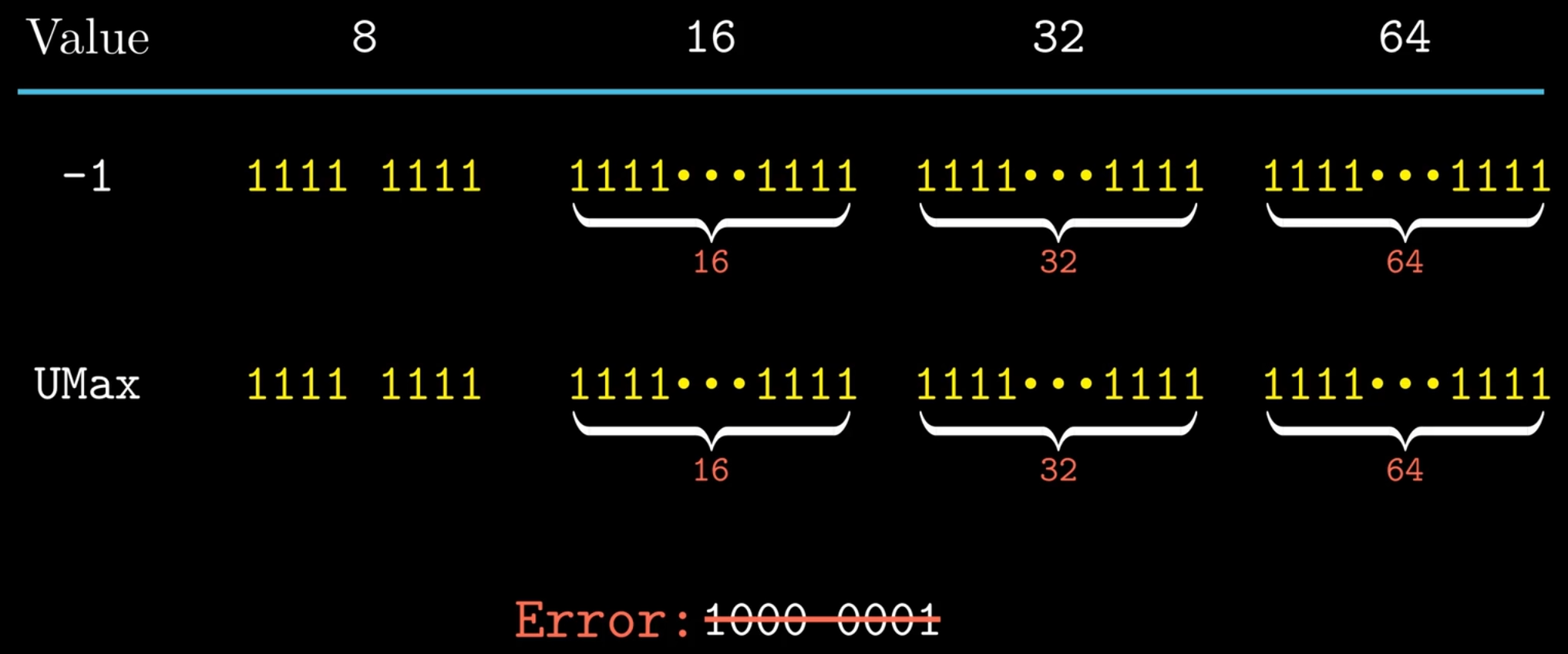
无符号数unsigned 与 有符号数signed 的相互转换
转换规则:位模式不变,但解释位的方式变了
| |
转换公式
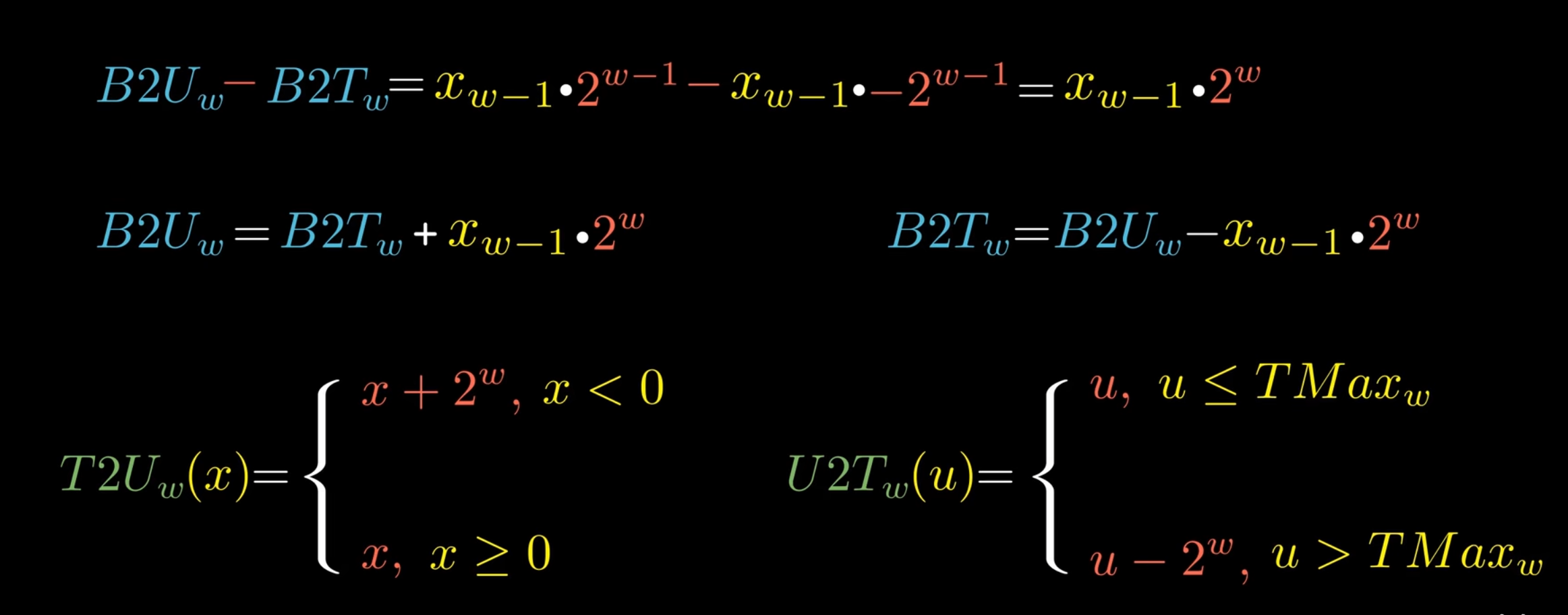
C 语言中如果进行 signed 与 unsigned 的运算,会隐式转换成 unsigned
数据类型的转换
小数据类型 -> 大数据类型:
unsigned 只需要在扩展的位补零即可
signed 需要执行符号位扩展(依据最高位)
大数据类型 -> 小数据类型
unsigned 截断超出位的部分
signed ,先与 unsigned 一样找出后 k 位,再将 unsigned 转化为 signed